Numbers

Numbers

The history of numbers is a fascinating journey that spans thousands of years and involves the development of various number systems, mathematical concepts, and cultural influences. Here’s a brief overview of the history of number:

Early Number Systems:

The earliest forms of counting were likely based on simple tally marks. Ancient civilizations, such as the Sumerians, Egyptians, and Babylonians, developed their number systems using symbols and hieroglyphs to represent quantities.

Babylonian Number System:

The Babylonians use a base-60 (sexagesimal) number system, which is believed to have influenced our modern system of measuring time (60 seconds in a minute, 60 minutes in an hour). They also developed methods for solving quadratic equations and calculating areas.

Roman Numerals:

The Roman numeral system  widely used in ancient Rome and remains recognizable today in certain contexts, such as clock faces and book chapters. It used a combination of letters to represent numbers.

Indian Numerals:

The Indian numeral system, also known as the Hindu-Arabic numeral system, introduced the concept of positional notation. It uses ten symbols (0-9) to represent all numbers, and the position of a digit determines its value. This system, along with the concept of zero, was introduced to Europe through the works of mathematicians like Fibonacci and al-Khwarizmi.

Development of Zero:

The concept of zero as a placeholder and as a number in its own right emerged in different cultures. The Indian mathematician Brahmagupta is credited with formalizing the rules for using zero in arithmetic.

Arabic Numerals in Europe:

During the Middle Ages, Arabic numerals gained popularity in Europe, replacing the Roman numeral system. This shift greatly simplified arithmetic calculations and contributed to the spread of mathematical knowledge.

Renaissance and Mathematical Advancements:

The Renaissance period saw significant advancements in mathematics, including the development of algebra and the use of symbols to represent mathematical operations. Mathematicians like Leonardo da Vinci, Johannes Kepler, and Galileo Galilei made important contributions.

Decimal Fraction System:

The widespread use of decimals and fractions for precise measurement and calculation became established during the Renaissance and Enlightenment periods.

Modern Number Systems:

The 17th and 18th centuries brought the formalization of the real number system, which includes rational and irrational numbers. Mathematicians like René Descartes and John Wallis contributed to this development.

Complex Numbers:

The concept of complex numbers, involving the imaginary unit “i,” emerged in the 16th and 17th centuries and became an essential part of mathematics, physics, and engineering.

Computing and Binary System:

The invention of computers in the 20th century relied heavily on the binary number system, which uses only two digits (0 and 1). This system underpins digital technology and information processing.

Throughout history, the evolution of number systems and mathematical concepts has been intertwined with the advancement of various cultures, civilizations, and fields of study. The development of number and their applications has played a crucial role in shaping our modern world.

Most common number system

The most common number system used in everyday life and mathematics is the Decimal Number System (Base-10). In this system, numbers  represented using ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The position of each digit in a number determines its value relative to powers of 10. This system is widely use for counting, arithmetic operations, measurements, and general numerical communication.

The Decimal Number System is the one most people are familiar with, as it is used for everyday calculations, financial transactions, measurements, and more.

Other number systems, such as binary (Base-2), octal (Base-8), and hexadecimal (Base-16), are also common in specific contexts, particularly in computing and digital technology:

• Binary Number System (Base-2): Used extensively in computer systems, binary represents numbers using only two digits: 0 and 1. It is the foundation of digital computing, where each digit represents a binary bit (either off or on).

• Octal Number System (Base-8): Octal is used occasionally in computing to represent groups of three binary digits (bits) more compactly. Each octal digit corresponds to three binary digits.

• Hexadecimal Number System (Base-16): Hexadecimal is commonly used in computing to represent binary data more concisely. Each hexadecimal digit corresponds to four binary digits, and it uses the digits 0-9 and letters A-F.

While the Decimal Number System is the most prevalent in everyday life, these other number systems play crucial roles in specialized fields like computer science, digital electronics, and data representation.

Classification of numbers:

 

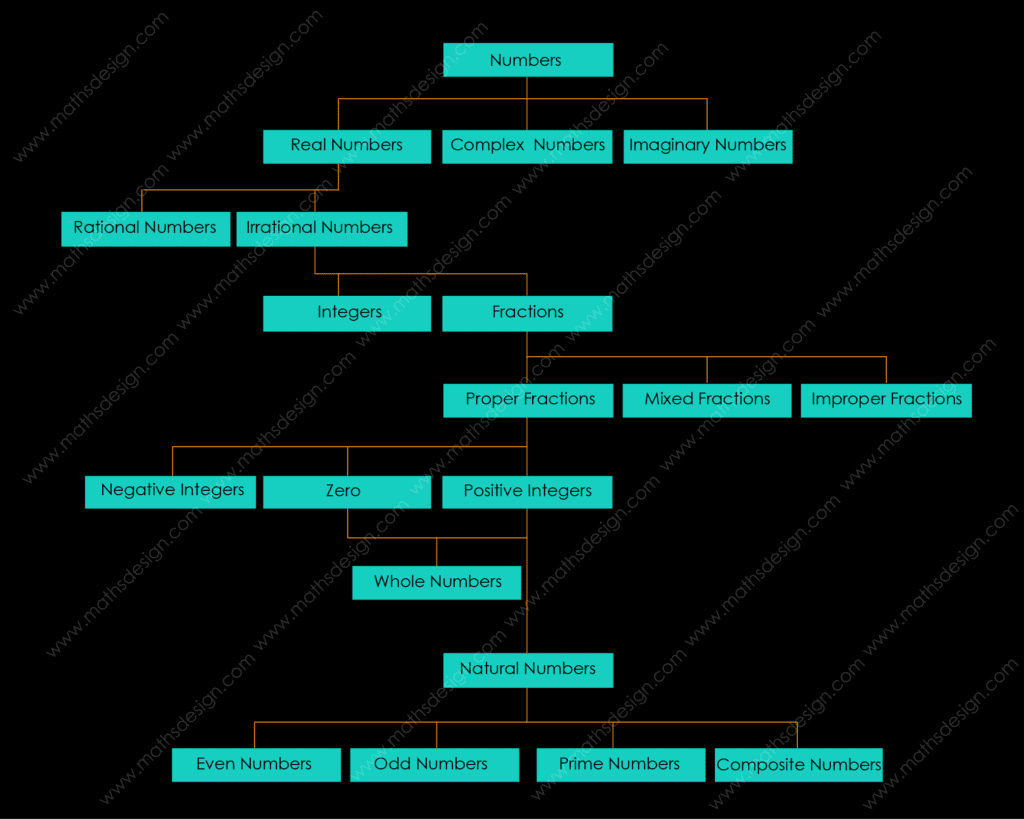
• Numbers

  • Real Numbers

    • Rational Numbers

    • Irrational Numbers

      • Integers

      • Fractions

        • Proper Fractions

          • Negative Integers

          • Zero

            • Whole Numbers

          • Positive Integers

            • Natural Numbers

              • Even Numbers

              • Odd Numbers

              • Prime Numbers

              • Composite Numbers

        • Mixed Fractions

        • Improper Fractions

  • Complex Numbers

  • Imaginary Numbers

 

www.mathsdesign.com

 

←BACK